- Does the statement double [] list; create an array of double elements?
Explain.
- State the value of the indicated element after execution of the given
declaration.
(a) a[4] after int [] a = nev int [20];
(b) b[23] after boolean [] b = nev boolean [50];
(c) c[2] after int[] c = {4,7,2,8};
(d) d[33] after double[] [] d = new double[100][];
- How much space (in bytes) would be required to store the elements
of the arrays created by the following declarations?
(a) double[] a = new double [10] ;
(b) byte[] b = new byte [30] ;
(c) int [] [] c = new int [10] [20] ;
(d) char[] [] [] d = new char[5] [4] [50] ;
- Given that list is a one-dimensional array of int values, write fragments
to print each value.
(a) the number of occurrences of the value zero,
(b) the product of all the elements,
(c) the sum of the positive elements,
(d) the minimum value.
- Given that table is a two-dimensional rectangular array, write fragments
to print each value.
(a) the number of elements
(b) the sum of the elements,
(c) the number of values that are multiples of three,
(d) the positive difference between the largest and smallest values
in the array.
- A polynomial in x of degree n is an expression of the form

The values a0, a1, ... ,an are called the coefficients of the polynomial.
Complete the definition of the method eval so that it returns the
value at x of a polynomial whose coefficients are stored in the array a.
public static double eval (double[] a, double x)
- Complete the definition of the method randomize whose header is
public static int[] randomize (int n)
The method should return an array of size n whose elements are the
values 0 ... n - 1 ordered randomly. As an example, randomize(5)
might return [4, 2, 0, 3, 1].
- Lacsap's Triangle is a triangular array of numbers in which each row
starts and ends with the row number and each interior value is the
sum of the two values on either side of it in the preceding row. The
following diagram shows the first five rows of Lacsap's Triangle.
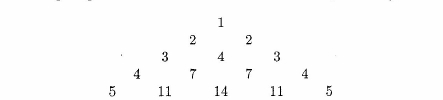
Write a program that asks the user for a positive integer and, once
a satisfactory value has been supplied, produces that many rows of
Lacsap's Triangle. For simplicity, do not try to print the triangle in
the symmetrical form shown here.
- A matrix is a rectangular array of values. The transpose of a matrix
is the matrix obtained by interchanging the rows and columns of the
original matrix. As an example,

Write a Java method called transpose that has one parameter, a two dimensional
array of int values. The method should return a two dimensional
array that is the transpose of the original array. Assume
that the parameter is a rectangular array.
- A magic square of order n is a square array containing the integers
1,2, ... ,n^2, each one used exactly once. The values in each row,
column, and diagonal must sum to the same value. As an example,
the following array is a magic square of order 3.

Write a boolean method isMagic that returns true if and only if its
single int [] [] parameter represents a magic square.
Projects
- The Sieve of Eratosthenes is the name given to an algorithm (An algorithm is a set of instructions for performing some process in a finite number
of steps.)for finding prime numbers (natural numbers having exactly two distinct
natural number divisors, one and themselves). The sieve starts by
considering all numbers greater than one as possible primes.
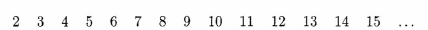
The first number in this list, 2, must be prime but all multiples of
two cannot be prime and hence can be eliminated from the list to
give us
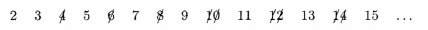
The next number still in the list, 3, must also be prime since it was
not eliminated when we found multiples of two. We can, however,
eliminate all multiples of three to obtain
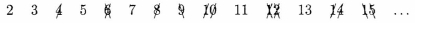
In the algorithm, this process continues (eliminating multiples of five,
seven, and so on) until it is no longer possible to eliminate any multiples
of values left in the table. The values that remain must all be
primes.
Write a program to implement Eratosthene's Sieve. The program
should ask the user for an upper bound and should then print all the
prime numbers less than or equal to that upper bound. In your
program, use a boolean array to maintain a record of the numbers
that are possible primes.
The output should have eight values per line with each value
right-justified in a field that is ten characters wide. You may find the
methods of the Out class shown in Appendix A useful for this.
- (a) The mode of a group of values is the value that occurs most
often in the group. A group may have more than one mode if
more than one value occurs with the maximum frequency. Such
a group is said to be multi-modal. (If there are exactly two
modes, the values are said to be bi-modal.) Write a program
that will read an unknown number of marks (out of 100) quitting
reading when a sentinel of -1 is read. The program should then
determine and print the mode(s) of the marks.
(b)Modify the program so that it also computes the median. If
there is an odd number of ordered values, the median is the
middle one; if there is an even number of values, the median is
the mean of the two scores adjacent to the middle. For example,
for scores of 51 68 68 73 84, the median is 68 while for scores of
51 68 68 73 84 90, the median is 70.5 (the mean of 68 and 73).
- Write a program that first reads the positions of a number of pieces
on a chess board and then reads the location of another position. A
piece can attack a position if it can move into that position. Your
program should determine which of the pieces can attack the given
position.
Chess is played on an 8 x 8 board whose rows are numbered from
1 to 8 (from the bottom to the top) and whose columns are lettered
from a to h (from left to right). In this problem you are only going
to be dealing with the following pieces:

The program should read the position of a piece by reading the piece
code, the column, and the row in that order, one character at a time.
It should continue to read the positions of pieces until the piece code
is X, indicating the position to be attacked. Assume that all input is
valid.
The output from the program should consist of a visual representation
of the chess board, as shown in the example. The diagram
should show the pieces in their positions, the position under attack
(denoted by the letter X) and dots in empty positions. The diagram
should be followed by a list of the pieces that can take a piece at the
location marked by the X. A piece is indicated by its code, its column,
and its row, in that order. The attacking pieces should be listed in
the following order: from the bottom row to the top row and from
left to right within a row. To determine whether or not a piece is
able to attack a position, ignore any other pieces that may be in the
way.
Sample input for the program is shown here. (Although all input is
shown on one line, when the program runs, each character should be
on one line.)

- Write a program that permits two players to play the game of Adjacency.
The game is played using X's and O's on an 8 x 8 board, initially
set up as shown in the following diagram in which dots indicate empty
squares. The rows and columns are numbered as shown.
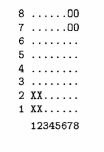
The first player begins by placing an X on an empty square. All
O's that are on adjacent squares are then replaced with X's. Two
squares are considered to be adjacent if they are one square apart
either horizontally, vertically, or diagonally. To illustrate, if the first
player puts an X on the square with coordinates (6,7), column 6 and
row 7, the resulting board configuration would be:

Play continues with the second player placing an O on an empty
square. The two players then take alternate turns. The game can
be terminated in one of two ways. The players may agree before the
first turn to terminate the game after a specific number of rounds or
play may continue until the board is filled. At the end of the game,
the player with the most pieces is the winner.
Your program should begin by asking for the names of the players,
determining the way in which they want the game to terminate,
and displaying the initial board. It should then repeatedly prompt
the players for their moves, displaying the updated board after each
move. If a player supplies invalid coordinates for a move, the program
should spot this and ask the player to re-submit valid coordinates
immediately. At the end of the game, the program should announce
either the name of the winner, if there is one, or print a message in
case of a tie.