6.8 Putting the Pieces Together
Throughout this chapter, we have been using Fraction objects to illustrate
our ideas. In this section we show how one might assemble and use the
various pieces that we have been developing.
Example 1
In the Fraction class that follows, we implement various constructors,
operations for performing arithmetic, a method, getFraction, for creating
new Fraction objects from input supplied by a user, a toString method
for printing fractions, and accessor methods that allow us to retrieve values
of private fields. The size method gives the magnitude of a fraction
while equals can be used to compare two fractions. The reduce method
is used to ensure that all fractions are maintained in reduced form with
non-negative denominators. It has been made private because it is not
needed outside the class; all Fraction objects are created and maintained
in reduced form within the class.
class Fraction
{
private int num;
private int den;
public Fraction ()
{
// Create an object representing 0/1.
num = 0;
den = 1;
}
public Fraction (int n, int d)
{
// Create an object whose value is n/d.
num = n;
den = d;
this. reduce();
}
public Fraction (Fraction f)
{
// Create an object identical to the parameter f
num = f.num;
den = f.den;
}
public Fraction plus (Fraction other)
{
// Create and return a Fraction object with value:
// this + other
Fraction result = new Fraction(num*other.den
+ den*other.num, den*other.den);
return result;
}
public Fraction minus (Fraction other)
{
// Create and return a Fraction object with value:
// this - other
Fraction result = new Fraction(num*other.den
- den*other.num, den*other.den);
return result;
}
public Fraction times (Fraction other)
{
// Create and return a Fraction object with value:
// this * other
Fraction result = new Fraction(num*other.num,
den*other.den);
return result;
}
public Fraction dividedBy (Fraction other)
{
// Create and return a Fraction object with value:
// this / other
Fraction result = new Fraction(num*other.den,
den*other.num);
return result;
}
public static Fraction getFraction (String prompt)
{
// Prompt the user for the fields of a fraction and
// return a new Fraction object (in reduced form).
Fraction result = new Fraction();
System.out.println(prompt);
System.out.println("numerator: ");
result.num = In.getlnt();
System.out.println("denominator: ");
result.den = In.getlnt();
result.reduce();
return result;
}
public String toString ()
{
// Return a string representing the implicit Fraction
// object. If the object represents an undefined or
// indeterminate value, return an appropriate string.
if (den != 0)
return num + "/" + den;
else if (num == 0)
return "NaN";
else if (num > 0)
return "Infinity";
else
return "-Infinity";
}
public int getNumerator ()
{
// An accessor method for the numerator field
return num;
}
public int getDenominator ()
{
// An accessor method for the denominator field
return den;
}
public boolean equals (Fraction other)
{
// Return true if and only if the fields of the implicit
// Fraction object are identical to those of other
return other!=null && num==other.num && den==other.den;
}
public double size ()
{
// Return the magnitude of a Fraction object
return Math.abs((double)num/den);
}
private void reduce ()
{
// Reduce the implicit Fraction object to lowest terms
// and ensure that the denominator is not negative.
// eliminate negative denominator
if (den < 0)
{
den *= -1;
num *= -1 ;
}
// store zero as 0/1
if (num == 0 && den != 0)
den = 1;
// store infinities as 1/0 or -1/0
if (den == 0 && num != 0)
if (num > 0)
num = 1;
else
num = -1;
// eliminate any common factors in num and den fields
for (int i = Math.min(Math.abs(num) ,den); i >= 2; i--)
if (num % i == 0 && den % i == 0)
{
num /= i;
den /= i;
}
}
}
|
|
Once we have created the Fraction class, we can then use it in programs
that manipulate fractions in an easy and natural way. The next two
examples show the use of some of the methods of the Fraction class.
Example 2
The following program prompts the user for two fractions and then finds
and prints their sum, difference, product, and quotient.
class FractionArithmetic
{
public static void main (String[] args)
{
Fraction first = Fraction.getFraction
("Enter the first fraction");
Fraction second = Fraction.getFraction
("Enter the second fraction");
System.out.println("sum is "
+ first.plus(second));
System.out.println("difference is "
+ first.minus(second));
System.out.println("product is "
+ first.times(second));
System.out.println("quotient is "
+ first.dividedBy(second));
}
}
|
|
If a user responds to the prompts by supplying fractions whose values are
3/4 and 5/8, the program will respond by printing
sum is 11/8
difference is 1/8
product is 15/32
quotient is 6/5
Example 3
The following program prompts the user for a value of n and then finds
and prints the value of the expression
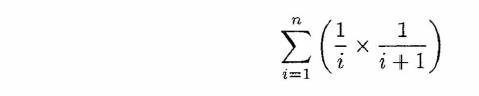class SeriesSum
{
public static void main (String[] args)
{
System.out.println("Enter a value of n");
int n = In.getlnt();
Fraction sum = new Fraction();
Fraction factor1 = new Fraction(1,1);
Fraction factor2 = new Fraction(1,2);
for (int i = 1; i <= n; i++)
{
Fraction term factor1.times(factor2);
sum = sum.plus(term);
factor1 = factor2;
factor2 = new Fraction(1,i+2);
}
System.out.println("Sum of " + n + " terms: " + sum);
}
}
|
|
If a user provides input of 10, the program will print
Sum of 10 terms is 10/11
In each of the last two examples, the resulting program contained
two classes: the Fraction class and another class containing the main
method. In programs containing more than one class, we can organize
the files containing these classes in a number of ways. One possibility is
to place each class in a separate file. In this case, the file containing the
class Sample should be called Sample.java. Alternatively, multiple classes
can be placed in one file. In this case, exactly one class should contain
the main method. The file name must refer to that class. For example, if
the class containing main is called Driver, then the file name should be
Driver.java.
The visibility modifier public can be used with classes, as it is with
methods and fields. If no visibility modifier precedes a class definition, then
the class has package visibility. If no package has been created, this means
that the class is visible from within the current directory. On the other
hand, if we declare a class to be public, then it can be seen from anywhere.
If a file contains more than one class, then only one can be declared public
and the file name must refer to this class. Combining some of these rules,
we can see that, if one of the classes of a multi-class file contains a main
method, then only this class can be declared public.
Exercises 6.8
Exercise 6.8
- The equals method of the Fraction class is used to test for equality
of Fraction objects. Why do we not simply use the == operator to
make this test?
- In the reduce method of the Fraction class, the index of the for
statement gets smaller with each iteration until it gets to two. Would
the method work correctly if the index started at two and became
larger on each iteration? Explain.
- Write a program that has a main method that uses the Fraction class
to solve the following problem: prompt the user for three fractions, a,
b, and c, compute the value of ab - c^2, print the result, and print the
sum of the squares of the numerator and denominator of the result.
- Write a program that uses the Fraction class to find and print, as
fractions in lowest terms, the values of the expression
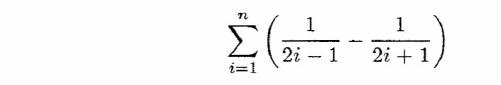
for n = 1,2, ... , 10.
- Use your results from the program of the previous question to conjecture
the value of
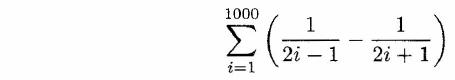
- Modify the toString method of the Fraction class so that, if the
magnitude of the numerator is equal to or greater than that of the
denominator, the method returns a string that has the form of either
an integer, if appropriate, or a mixed fraction. The table shows
examples.
|
|