Exercise 5.9

Some methods return values while others do not.
1. What is the difference between the forms of the definition of each of these kinds of methods?
2. What is the difference between the calls to each of these kinds of methods?
Explain the difference between an argument and a parameter.

What is the scope of a parameter of a method?

In the method outline shown here, state which variables can be used at each numbered line.

public static int sample (int a, int b) { // 1 int c; ... // 2 for (int d = 0; .. ) { ... // 3 int e; ... // 4 } ... // 5 { int f; ... // 6 } int g; ... // 7 }

1. Write a definition of a method norm that has three double parameters, x, y, and z. The method should return, as a double value, the value of the expression [x² + y² + Z²]^1/2
2. For variables a, b, and c, write statements that use norm to assign to the indicated variables the values of each of the following expressions:

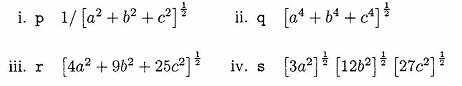Write a boolean-valued method isSquare with a single int parameter, n. The method should return the value true if and only if n is the square of some integer.

Complete the definition of the method digit with header
public static int digit (int n, int position)
so that the method returns the value of the digit that is position places from the right in the decimal representation of n. As examples,
```
   digit (763,0) should return 3
   digit (8574,2) should return 5

   digit (78,4) should return 0 
```
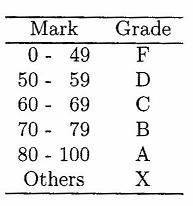
Write a character-valued method convertToGrade that has an int parameter mark. The method should return the grade that corresponds to mark according to the following table.
Write a method printTriangle that has a char parameter c and an int parameter n. The method should print a triangular pattern with the perimeter consisting of the character c and the interior (if there is one) consisting of blanks. As an example, the call printTriangle('*',5); should produce output of the form
You may assume that the value of n is positive.

1. Write a definition of a method leastFactor that has one int parameter, n. If n > 1, the method should return the value of the smallest prime factor of n; otherwise, it should return the value zero.
2. Write a program that uses leastFactor to find and print all the prime factors of numbers read as input. For example, given input of 12, the program should note that the prime factors are 2, 2, and 3. The program should be interactive, prompting the user for values and processing them until a value less than one is supplied by the user.

Write a method dayNumber that determines the number of days in a year up to and including the current day. The method should have three int parameters: year, month, and day. If the value of any parameter is invalid, the method should print a warning message and return the value zero. The table gives some examples of the action of the method. Accept any non-negative year as being valid. You may want to assume the existence of a method numberOfDays that returns the number of days in a given month of a given year.

Triangles can be classified in a number of ways by considering the relative sizes of either their sides or their angles. Using side classifications, a triangle is equilateral if all sides are equal; it is isosceles if exactly two sides are equal; it is scalene if no sides are equal. Using angle classifications, a triangle is a right triangle if its largest angle is a right angle; it is obtuse if its largest angle is greater than a right angle; it is acute if its largest angle is less than a right angle. If the sides of a triangle are known, Pythagoras' Theorem can be used to classify the triangle as right, obtuse, or acute.
Write a program that will read an arbitrary number of sets of three integers. The program should prompt the user for sets of numbers and process them until the user submits the numbers 0 0 0. For each set of three numbers, the program should first print the values read. It should then decide whether or not the three numbers could represent the lengths of the sides of a triangle. If the numbers could not represent the lengths of sides of a triangle, an appropriate message should be printed. If they could, then the program should determine and state into which of the above classes the triangle would be placed. If the user provided input of
```
   3 5 4
   5 2 5
  -7 1 2
   0 0 0
```
then the program should produce output something like the following:
Nim is a two-player game in which players take turns picking up sticks. The game begins with various numbers of sticks in a number of piles. On any turn, a player must choose a pile and remove one or more sticks from that pile (up to the number of sticks in the pile). The object of the game is to force your opponent to pick up the last stick in the last pile.
Write a program that allows two people to playa game of Nim. The program should start by creating four piles of sticks, each with a number of sticks that varies randomly from four to eight and displaying the piles on the screen. The program should then prompt the first player to remove a number of sticks from a pile. Once that player has provided valid input, the program should then adjust the piles and display the new configuration. This process should continue until one player has won the game, at which time the computer should print a congratulatory note to the winner. At the end of each game, the computer should start a new game if the users state that they want to do so. Once the users state that they are done, the computer should print the number of games won by each player.

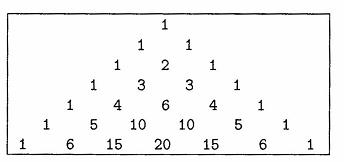
Pascal's triangle is a triangular array of numbers named in honour of the French mathematician Blaise Pascal. The first few rows of the triangle are:
The triangle can be extended as far as we please. The values of the entries in any row can be obtained in a number of ways. One way is to note that, in any row, the first and last entries both have the value one while the value of each interior entry is the sum of the values in the row above it, to its left and right. As examples, in the last row shown, 6 = 1 + 5 and 15 = 5 + 10. The values can also be obtained without reference to other values. If we let the symbol represent the number of ways of choosing r items from n different items, then the entries in the first few rows of Pascal's triangle are:
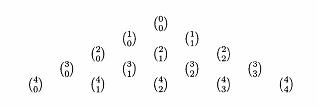The value of can be calculated using the formula:
where the symbol n! is read as n factorial. The value of n! can be found using the formula:
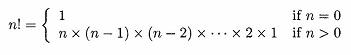Write a program that prints portions of Pascal's triangle. The program should repeatedly ask the user to supply the number of rows in the triangle, terminating when the user supplies the value zero. In printing a triangle, the first value in the last row should appear in the first column and each preceding row should start printing three spaces further right. The number of spaces between entries in a row should be adjusted so that values are aligned correctly from row to row. For example, if the user supplies input of 7, the program should print the following triangle. In the bottom row of the triangle, there are five spaces between the first 1 and the first 6 but only four spaces between the first 6 and the first 15. In this way, the last digit of 15 is aligned with the 4 and 1 above it.
Your program should be able to print up to twenty rows of Pascal's triangle. (Larger triangles contain entries that are more than five digits long; they will not fit in the format specified for the problem.) If a user specifies a number of rows greater than twenty or less than zero, the program should reject the value gracefully. For large triangles, your output device may not be able to print all the characters in some rows on a single line. In such cases, the output of one row will automatically wrap around to the next line. Do not worry about this behaviour.