2.6 Using Math Methods

We have already encountered the classes In and System where we found methods for performing input and output. To assist us in doing mathematics beyond basic arithmetic, Java has a large group of methods contained in a class called Math. In this section we will examine some of the most frequently used methods in the Math class. To use any of the methods in Math, we must identify them as being in that class by including the class name as part of the method name. Each of these methods computes a value; we often speak of this value as the value returned by the method.

Math.abs

The method Math.abs determines the absolute value of an expression. The expression on which Math.abs operates is called the argument of the method. To use the method, the argument is enclosed in parentheses, just as it is in a function in mathematics. The argument can be of any primitive type other than boolean. The type of value returned by the method corresponds to the type of its argument. If the argument is of type int, long, float, or double, the method will return a value of that type. If the argument is of a type narrower than int, the method will return a value of type int. (See Chapter 5 for a more detailed discussion of arguments.)

Example 1

  1. Math.abs(-4) => 4
  2. Math.abs(2.7f) => 2.7f
    3.
  3. Math.abs(-8.2e-4) => 8.2e-4
    4.
  4. Math. abs (-456L) => 456L

Math.sqrt

The Math.sqrt method returns the positive square root of the argument given to it. The method will take a numerical value of any type as argument. It returns a value of type double. If the method is given a negative value, it will return the value NaN.

Example 2

  1. Math.sqrt(4) => 2.0
    2.
  2. Math.sqrt(7.0) => 2.6457513110645907
    3.
  3. Math.sqrt(-5.0) => NaN
    4.

To calculate small positive powers of numbers, it is most efficient to simply use the multiplication operator, *. In addition, to calculate x5 = √x, it is best to use the Math.sqrt method. However, to calculate other powers, we can use the method Math.pow that will evaluate xy. The method always returns a double value, no matter what types the arguments are. A call of the form Math.pow(a,b), if a and/or b are not double values, will first determine the double equivalent of a and b. It will then determine and return the value of ab as a double value. If the exponent is not an integer and the base is negative, the method returns NaN.

Example 3

  1. Math.pow(8,1.0/3.0) => 2.0
    2.
  2. Math.pow(2,10) => 1024.0
    3.
  3. Math.pow(-32.0,0.2) => NaN
    4.
  4. (int)Math.pow(100,0.25) => 3
    5.

Math.max, Math.min

The method Math.max takes two arguments and returns the larger of the two. As with Math.abs, the arguments to Math.max can be of type int, long, float, or double. If the two arguments are of the same type, the method will return that type; if they are of different types, the method will return a value of the wider type. The method Math.min returns the minimum of two values. It operates in a way exactly analogous to that described for Math.max.

Example 4

  1. Math.max(-3,2) => 2
  2. Math.max(3.4f,5.3f) => 5.3f
  3. Math.max(7,3L) => 7L
  4. Math.max(-9e-4,-1.1e-6) => -1.1e-6
  5. Math.min(8,7) => 7
  6. Math.min(1.5f ,2.0) => 1.5
  7. Math.min(-4.7,-9.3) => -9.3
  8. Math.min(18,6.7) => 6.7
    9.

Math. round, Math. ceil, Math. floor

The Math.round method rounds a floating point value to the nearest integer. It returns an int value if its argument is float and returns a long value if its argument is double. The Math.ceil and Math.floor methods both take a double argument and return a double value. Math.ceil returns a double that has the smallest integer value that is not less than its argument while Math.floor returns a double that has the largest integer value that is not greater than its argument.

Example 5

  1. Math.round(2.7) => 3L
  2. Math.round(-2.13f) => -2
  3. Math.floor(8.0) => 8.0
  4. Math.ceil(-5.47) => -5.0
  5. Math.round(4.5f) => 5
  6. Math.floor(21.94) => 21.0
  7. Math.ceil (18.8) => 19
  8. Math.ceil(-5.0) => -5.0
    9.

The Math.round method can be adapted to rounding to a precision other than the nearest integer. To do this,we can first apply a scaling factor to the original value, round the result to the nearest integer,and then reverse the effect of the scaling.

Example 6


The following program reads and rounds a double value to the nearest hundredth, a precisions pecifiedby the constant value of that name. 
class Roundoff
{
   public static void main (String[] args)
   {
      final double PRECISION = 0.01; //rounding precision
      double inValue; //value to be rounded
      double roundedValue; //value after rounding
            
      System.out.println("Please supply a value for rounding");
      inValue = In.getDouble();
      roundedValue = Math. round (inValue/PRECISION) *PRECISION;
      System.out.println("Input value: "+ inValue);
      System.out.println("Rounded value: " + roundedValue);
   }
}

Math.random

The Math.random method takes no argument. It returns a double, a random value x in the interval 0 <= x < 1. By combining this method with other methods and operations, we can generate random values suitable for a wide variety of applications. As an example, suppose that we wish to simulate the throwing of a fair die - one for which each of the six faces on the die is equally likely to turn up. We can do so by performing the following operations.
We can begin by calling the method Math.random to generate a value distributed randomly in the interval 0 <= x <= 1.
Multiplying this by 6, we expand the range to get a value distributed randomly in the interval 0 <= x <= 6.
Next, casting this result as an int, we chop off any fractional part to obtain a random integral value in the range 0, 1, ... ,5.
Finally, adding one gives us a random integral value in the desired range: 1, 2, ... ,6.
All of these operations can be performed in one step with the statement 
int dieRoll = (int)(6 * Math.random() ) + 1;

Constants

In addition to its methods, the Math class also has two important double constants: Math.PI and Math.E. The constant Math.PI gives the value of π = 3.14159... to 16 significant digits while Math.E gives the value of e = 2.71828... to 16 significant digits.

Trigonometric Methods

The class has a number of trigonometric methods, including Math.sin, Math.cos, Math.tan, Math.asin, Math.acos, and Math.atan. Java, like most programming languages, prefers to work in radians rather than degrees.To convert from one measurement system to another, you can use the relationship
π radians = 180 degrees
The methods Math.sin, Math.cos, and Math.tan each take a single argument, representing the radian measure of an angle. They return the sine, cosine, and tangent of their arguments, as double values.

Example 7

  1. sin 60¡ = 0.866025 ... Math.sin(Math.PI/3) => 0.866025 ...
  2. cos 5¡ = 0.996194... Math.cos (5*Math. PI/180) => 0.996194 ...
  3. tan45¡ = 1 Math.tan(Math.PI/4) => 1.0
  4. cos 180¡ = -1 Math.cos(Math.PI) => -1.0
  5. cot 0¡ is not defined 1/Math.tan (0) => Infinity

The methods Math.asin, Math.acos, and Math.atan determine values of the inverse trigonometric functions: arcsin (sin), arccos (cos-1), and arctan (tan-1). The method Math.asin returns, as a double value, the measure in radians of an angle whose sine is the argument. The others behave similarly.

Example 8

  1. arccos0 = π/2 Math.acos(0) => 1.5707963 ...
  2. arctan1 = π/4 Math.atan(1) => 0.7853981...
  3. arcsin Math.asin(Math.sqrt(3)/2) => 1.047197 ...

Exponential and Logarithmic Methods

The class also contains the methods Math.exp for determining ex, and Math.log for determining In x, the logarithm of x to the base e.

Example 9

  1. e = 2.71828\8... Math. exp (1) => 2.7182818...
  2. In e = 1 Math.log(Math.E) => 1.0
  3. e3 = 20.0855369... Math.exp(3) => 20.0855369...
  4. In 1 = 0 Math.log(1.0) => 0.0
  5. In(-1) is not defined Math.log(-1.0) => NaN


This section has not given a complete listing of the methods of Java's Math class. A full list with notes on all the elements of the class can be found at Sun's web site (http://java.sun.com/). At the site, to locate information on any feature of the Math class, follow links first to the Application Programming Interface or API. The API is a collection of hundreds of classes that add functionality of various kinds to Java. The classes of the API are organized into groups called packages. The Math class is in the package called java.lang (not in the package java.math). Once you are at the index page of the API, you can either locate a class directly by its class name or find it indirectly by first going to its package and then finding the class within the package. At the time that this was written, the page containing the index of the API for Java 2 was located at http://java.sun.com/j2se/1.4/docs/api/

Now that we can do mathematics in Java, we can write many useful programs. The next example illustrates a program structure that we will see frequently. The program obtains input, does some calculation, and produces some output.

Example 10

For a simple pendulum, the length of time for one swing (the period) is determined by the pendulum's length and the force of gravity. If we assume that gravity is constant anywhere on the surface of the earth, then the period of a pendulum is determined by its length. The formula connecting period and length is

where the period, P, is measured in seconds, the length, L, is measured in metres, and g is the acceleration due to gravity - 9.8 m/s2. The following program uses this formula to determine the period of a pendulum of a given length. 
class Pendulum
{
   public static void main (String[] args)
   {
      final double G = 9.8; 
      // acceleration due to gravity
      
      System.out.println("Give pendulum length in metres");
      double length = In.getInt();
      
      //find period, rounded to nearest tenth of a second
      double period = 2*Math.PI*Math.sqrt(length/G);
      period = Math.round(10*period)/l0.0;
      System.out.println("For a length of " + length + " m,"
            + " pendulum's period is " + period + " s.");
   }
}


Exercise 2.6

  1. State the value and type of each expression.
    1. Math.abs(-S)-Math.abs(-7)
    2. Math.abs(-1e-1) + Math.abs(-2e-2)
    3. Math.sqrt(0.0064)
    4. Math.sqrt(Math.pow(2.7,2)
    5. Math.round(3.499)
    6. Math.max(1.5e-2,0.095)
    7. Math.ceil(4.002)
    8. Math.min(-5,1.0)
    9. Math.floor(7.99)
    10. Math.ceil(-2.73)
    11. Math.pow(16,O.25)
    12. Math.pow(4,-2)
    13. Math.round(1.49 + 0.1)
    14. Math.round(1.49) + 0.1
      15.
  2. Write as Java expressions.
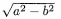    2. π(x6 - y6)
    3. 4/3π r3
    4. |z4-1|
    5. ln |1+x|
    6. x2ex
  3. A student incorrectly attempted to produce a random value uniformly distributed over the set {1,2,...,6} using the expression 
    6*(int)Math.random() + 1
  4. Write a statement that will make the int variable result take on a random value uniformly distributed over the given set.
    1. {1, 2, 3, , 10}
    2. {1, 2, 3, , 52}
    3. {5, 10, 15, , 100}
    4. {-5, -4, -3, , 5}
    5. {100, 110, 120, , 300}
    6. {a, a + b, a + 2b,..., a + kb} where a, b, and k are integers.
  5. Write a statement that will assign the char variable randChoice a random value from the set {'A', 'B', 'C', 'D', 'E'}.
  6. Write a statement that will assign the double variable randVal a random value from the set {1.00, 1.25, 1.50, ... , 4.00}.
    1. Write a statement that will assign the int variable dodecaRoll a random value that could result from the rolling of a fair twelvefaced die with faces numbered from one to twelve.
    2. Write a statement that will assign the int variable doubleRoll a random value that could result from noting the sum obtained by rolling a pair of standard, fair dice with faces numbered from one to six.
  8. Find the value of each expression.
    1. Math.sin(Math.PI/6)
    2. Math.cos(Math.PI/3)
    3. Math.cos(0)
    4. Math.atan(0)
    5. Math.tan(Math.atan(0.5))
    6. Math.asin(Math.sin(1))
      7.
  9. Write Java expressions for each of the following.
    1. sin 45°
    2. cos 120°
    3. tan 24°
    4. sec 18°
    5. csc l60°
    6. cot 15°
    7. arctan 2
    8. arcsin 0.5
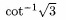    10. sec-1(1.5)
  10. Write an expression that could be used to find the value of log10x.
  11. In this section, we showed a program that rounded a value to the nearest hundredth. How would that program have to be modified to round values to
    1. the nearest tenth?
    2. the nearest thousand?
  12. Airport runways are often given numbers determined by the direction in which planes travel as they move along the runways. The number of a runway is found by taking the bearing in degrees (to the nearest ten degrees) and dropping the final zero. For example, a runway with a bearing between 265° and 275° would have a runway number of 27. Write a program that asks the user for a bearing (from 0° to 360°) and then determines the corresponding runway number.
  13. Write a program that asks for a length of time in hours and then converts this measurement to hours, minutes, and seconds. For example, input of 38.47 should produce output similar to the following:
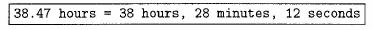