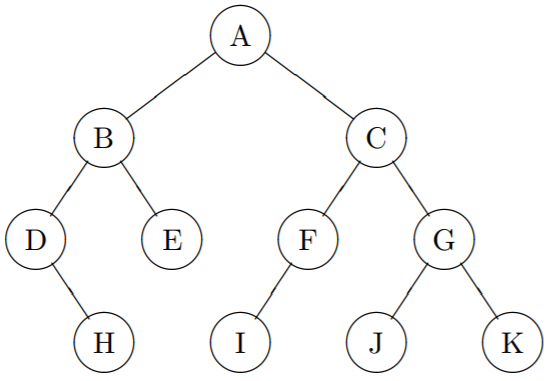
Example 1
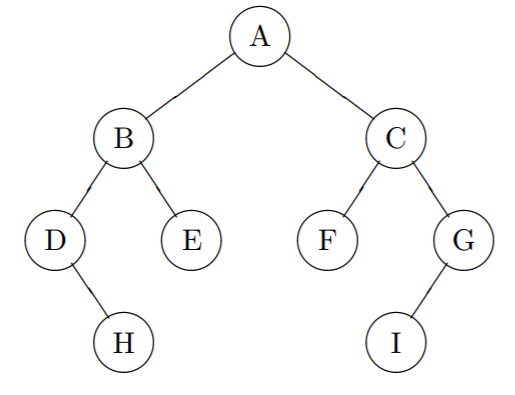
The following diagram shows a binary tree containing the nodes A, B, ..., I.
Although linear lists are useful for many applications, more complex structures are often required. In this section, we will begin to examine another extremely useful data type -- the binary tree.
The following diagram shows a binary tree containing the nodes A, B, ..., I.

In talking about trees, the terminology is taken partially from family trees and partially from organic trees. Considering the tree shown in Example 1 as a family tree, the nodes F and G are the children of C, with F being the left child and G being the right child. Since F and G both have C as a parent, they are siblings. From organic trees, we get the terms root and leaf. The node A is the root of the tree while H, E, F, and I are the leaves. (In computer science, trees usually grow upside down.) The root is the only node that has no parent while the leaves are the only nodes that have no children.
The nodes B, D, E, and H form the left subtree of the tree while C, F, G, and I form the right subtree. Each subtree is itself a tree so that, for example, B, D, E, and H form a binary tree whose root is B.
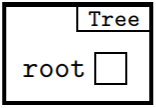
To implement a binary tree, we can use arrays but, in this text, we will only be looking at linked allocation. To start a Tree class, we need one field, a reference to the root of a tree.
class Tree
{
private Node root;
}
We present objects of type Tree by diagrams like the following:
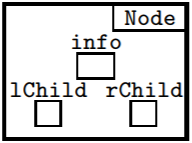
A node of the tree will need three fields: a link to the node's left child (or null if there is no left child), a link to the node's right child (or null if there is no right child), and an information field. As with linked lists, this field will, in practice, be a reference to some object but, for demonstration purposes, we will simply store integers into our info fields. To start our Node class, we give it the required fields and a simple constructor:
class Node
{
int info;
Node lChild, rChild;
Node (int i, Node l, Node r)
{
info = i;
lChild = l;
rChild = r;
}
}
Objects of the Node class will be represented by diagrams like the following:
Using the Tree and Node classes, the implementation of the binary tree shown in the previous example would have the structure shown in the next diagram. The nodes are labelled with the same letters used in the previous example.

Operations on binary trees are most easily performed using recursion. As we saw in the previous section, it is useful, if we want to develop recursive algorithms for processing a data structure, to first look at that structure recursively. We can do this here by defining the structure of the ADT binary tree as: a set of nodes that is either empty or, if not empty, contains a node called the root together with two disjoint binary trees: the left subtree of the root and the right subtree of the root.
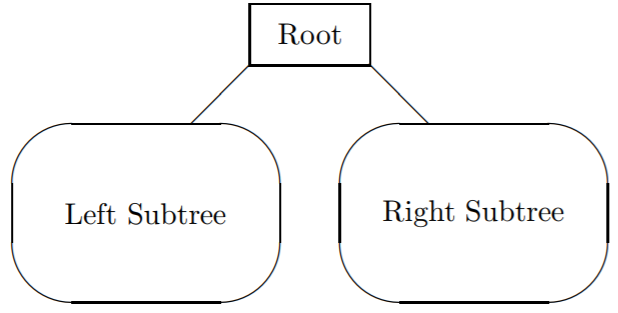
Recursive algorithms for operating on binary trees reflect this form by processing the root directly and processing the left and right subtrees recursively with an empty tree acting as a stopping condition on the recursion.
As a simple illustration of recursion with a binary tree, consider the problem of performing a traversal of a tree. In a traversal, we want to visit each node of the tree, performing some task such as printing the data in each node as we carry out our visitation. If we want to traverse a binary tree, there are many possible orders in which we can visit the nodes. (For a tree containing ten nodes, for example, there are 3,628,000 possible orderings.) Of these many orderings, only a few are commonly used. Three of the most common orderings are very similar. In each of them, the left subtree is traversed before the right subtree. The only difference among the three is the point at which the root is visited. The outlines and names of the orderings are shown in the table.
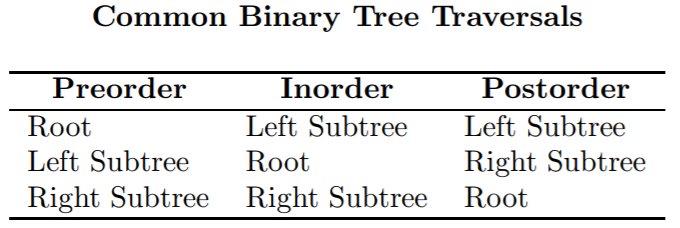
The names are derived from the point at which the root is visited relative to the traversal of the two subtrees: pre (before), in (between), or post (after) the subtrees.
A recursive algorithm for an inorder traversal of a binary tree could take the following form.
To TRAVERSE THE TREE
if the tree is not empty
TRAVERSE THE LEFT SUBTREE
visit the root
TRAVERSE THE RIGHT SUBTREE
As we did for recursive operations on linked lists, we can break up the task here into two parts: a non-recursive method in the Tree class to process the case of an empty tree and a recursive version in the Node class to process non-empty binary trees.
Suppose that a binary tree is implemented using the data structure in the previous example. To print info fields of such a tree using an inorder traversal, we could use the following methods.
First, in the Tree class,
public void inPrint()
{
if (root != null)
root.inPrint();
}
Then, in the inner Node class,
void inPrint() { if (lChild != null) // print non-empty left subtree lChild.inPrint(); System.out.println(info); if (rChild != null) // print non-empty right subtree rChild.inPrint(); }
public int sum() { if (root == null) return 0; else return root.sum(); }