10.7 Comparing Algorithms

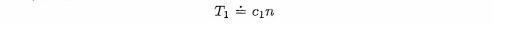
In this chapter we have looked at two searching algorithms and four sorting algorithms. We now turn our attention to the problem of comparing these algorithms, to try to decide which is "best".

Before we start comparing the efficiency of algorithms, we must agree on some way of measuring efficiency. We do not want a measure that is dependent on the language in which the algorithm is coded or on the machine on which the program is executed. Instead, we want a measure of performance that depends only on the "size" of the problem. For most problems, there is usually some clear measure of the size. For searching and sorting lists of values, the size of a problem is usually taken to be the number of elements in the list.

Once we have a measure of the size of a problem, we then want to determine how a solution to a problem grows relative to the growth in its size. To measure growth of a solution, we often compare size to either the space required by the solution or the time required by the solution. (Frequently it turns out that there is a tradeoff between these two quantities; an algorithm that is relatively fast will use more space than one that is slower.) In this text, we will not be concerned with space considerations; we will restrict ourselves to a (somewhat informal) study of growth in time relative to the growth in size of our problems.

To begin, consider the sequential search algorithm developed in the first section of this chapter. Most of the time spent by the search is devoted to comparisons between the item sought and elements of the array being searched. If there are n elements in the array, then the maximum number of comparisons that would be required is n. If, on one machine, a single comparison takes C_l time units, then, since most of the time taken by execution of the algorithm is devoted to comparisons, the total time for the search will be roughly C_l x n time units. If we let this time be T_l time units, then we have

If we change computers or programming languages, we might find that a single comparison now takes C₂ time units. In this case, the total time, T₂, will be given by:

In either case, the amount of time required by the sequential search is approximately proportional to n. If we let the time be T, then we could write this approximate proportionality in the form

Instead of this notation, however, we will usually write the relationship in the form

Reasonably enough, the use of 0 is called big oh notation. We can read the statement as "T is big oh of n" or "T is order n" We should confess that we are, in fact, not really telling the truth about big oh notation. More advanced courses, dealing with analysis of algorithms, give a more precise definition.¹ For our purposes, however, we can think of the following relationships for a function f as being equivalent.

In making our analysis of the time required by a sequential search, we supposed that all the elements of a list would have to be examined. This is known as a worst case analysis. If we wanted to examine the average time required by a sequential search, we might make the assumption that the data are randomly ordered so that, on average, we would have to examine about half of the elements to terminate a successful search. If the worst case gave

then the average case (under our assumptions) would be

This means that T is still approximately proportional to n. Using our big oh notation, we have, once again,

Analysis of the performance of binary search requires a somewhat different approach. As with sequential search, we use the number of comparisons to obtain an approximation of the rate of growth of time, T, as the size, n, of a list increases. Again, as with sequential search, in the worst case we must continue to examine elements until the size of the list is reduced to zero. Unlike the case with a sequential search, however, each time we make a comparison with a binary search, we eliminate approximately half of the remaining items. We let the total number of comparisons required for a list of size n be C_n. Since one comparison eliminates approximately half the elements in the list, we have

Similarly

Substituting the second equation in the first gives

After one more comparison, we have

After k comparisons, we have

To actually determine the value of Cn from this equation, we note that exactly one comparison is required for a list of size one. Thus, if n/2^k = 1, C_n/2^k = 1 and hence

Now, to obtain C_n in terms of n, we solve the equation n/2^k = 1 for k.

Because logarithms with base 2 appear so often in analysis of algorithms, we often abbreviate the expression log ₂ n as simply 19 n. Substituting this value for k in our equation for c_n gives us

Since the time required by the search will be roughly proportional to the number of comparisons, we have, finally

To analyze the performance of selection sort we note that, once again, the primary activity during execution of the sort is comparison of items. The first pass requires n-1 comparisons to find the largest item, the second pass requires n - 2 comparisons, the third pass requires n - 3 comparisons, and so on until the last pass requires only one comparison. The total number of comparisons is

(n - 1) + (n - 2) + (n - 3) + ... + 1

and we know from mathematics that the sum of this arithmetic series is

(1/2)(n²-n)

As with our searches, most of the time used by selection sort is spent doing comparisons. If we let T units be the total time taken by selection sort, then

Since we are dealing here with proportionalities, we can eliminate the constant multiplier to obtain

We can simplify this expression even further. To do so, let us compare values of the expression n² - n with n².

As you can see from the table, as t_i gets larger, the effect of subtracting n from n² becomes (in relative terms) almost insignificant. For large values of n, the expressions n² - n and n² are relatively very close as indicated by the ratios in the last column. In such a situation, where one term of an expression dominates any others, our big oh notation allows us to simplify our description of an algorithm's behaviour by eliminating the non-dominant terms. For the selection sort we can, therefore, write

T is O(n²)

In addition to comparing items, sorting also involves moving them around if they are out of order. Using a selection sort on a list with n items, we may have to perform n - 1 swaps to get items into their correct positions. If each swap takes s time units, then the total time for all swaps is s(n - 1). This operation is, therefore, O(n). Since the comparisons are O(n²), the time for comparisons dominates the total time and so selection sort is O(n²). Both insertion sort and bubble sort are also O(n²) algorithms but insertion sort usually requires more data movement than selection sort and bubble sort usually requires far more data movement, making it slower than either selection sort or insertion sort. Shellsort can provide dramatic improvement in running time over any of the other three sorts that we have studied. Although no exact analysis of the performance of Shellsort has yet been possible, it has been found that with a good sequence of jump sizes, the time taken by Shellsort is approximately O(n^1.25). There are a number of sorts that have even better performance than Shellsort. We will study one such sort, quicksort, when we examine a technique called recursion in Chapter 11. Although our performance measures are not linked to specific computers or programming languages, they can help us to determine actual performance times. This is illustrated in the next example.

A selection sort running on a particular computer requires 0.003 s to sort 200 items.² Estimate the time that the sort would require on the same machine to sort 8000 items. Since selection sort is O(n²), the time taken by the algorithm is roughly proportional to n² so that

where k is a constant for a particular environment. For two separate runs on the same computer, we would then have

Combining these equations gives

Substituting the values that we know, we get

The sort would take about 5 s to sort 8000 items.

Exercise 10.7

If an algorithm is known to be O(n²) and it takes t s to process a problem of size n, about how long would it take (in the same computing environment) to process a similar problem of size
(a) 2n? (b) 3n? (c) 5n? (d) 10n?
If an algorithm is known to be O(n³) and it takes t s to process a problem of size n, about how long would it take (in the same computing environment) to process a similar problem of size
(a) 2n? (b) 4n?
Binary search is known to be O(lg n). Suppose that a binary search requires c comparisons (in the worst case) to search a list of size n. What is the maximum number of comparisons that the search would require for a list of size
(a) 2n? (c) 8n? (b) 4n? (d) 64n?
Suppose that, in a certain environment, selection sort requires 0.06 s to sort a list of length 500.
(a) Estimate the time that it would require to sort a similar list of length 50 000.
(b) Estimate the number of items that could be sorted in one hour.
Suppose that, in a certain environment, Shellsort requires 0.004 s to sort a list containing 1000 items.
(a) Estimate the time that it would take to sort a similar list of length 100 000.
(b) Estimate the number of items that could be sorted in one second.
Although Shellsort is more efficient than straight insertion sort, insertion sort might be faster for short lists because the algorithm is simpler. Suppose that, on a particular machine, both insertion sort and Shellsort require 0.05 s to sort 200 items. Find the approximate amount of time each one would take to sort 100 000 items.
Draw graphs showing the number of comparisons that would be required (in the worst case) by each of the following algorithms.
(a) sequential search
(b) binary search
(c) selection sort