6.4 Comparing and Displaying Objects

Before looking at new operations, let us recall the way that assignment statements work with reference variables.

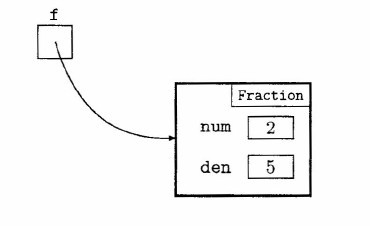
Example 1 Suppose, once again, that we are using our Fraction class and that we have created an object f by writing Fraction f = new Fraction(2,5); to create the object shown in the next diagram If we now write Fraction g = f; this copies the value from the reference f to the reference g, producing the result shown in the next diagram where f and g refer to the same object.

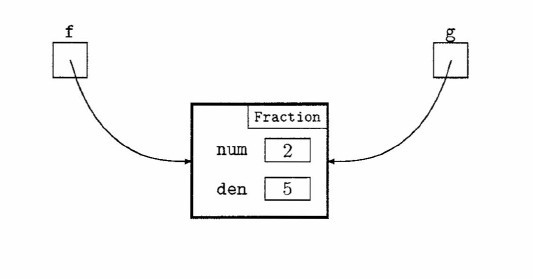If we wanted f and g to refer to different objects that represented the same fraction, we would have had to proceed somewhat differently.

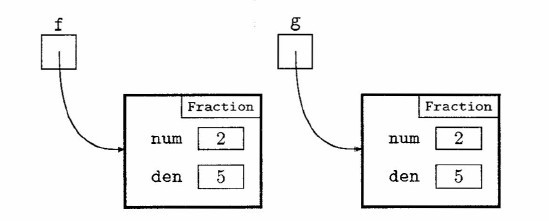
Example 2 If we first create f as we did in the previous example, and then wrote Fraction g = new Fraction(f) ; this would create a new object whose instance fields have the same values as those of the original. (We are assuming here that we have written an appropriate constructor, as shown in Example 2 of Section 6.3.) The result of this statement is shown in the next diagram. In this situation, if we were to write g.setNum(1); this would change the num field of the object to which g refers. Since f now refers to a different object, that object would not be changed.

In comparing objects, we must again be conscious of the fact that object variables are references.

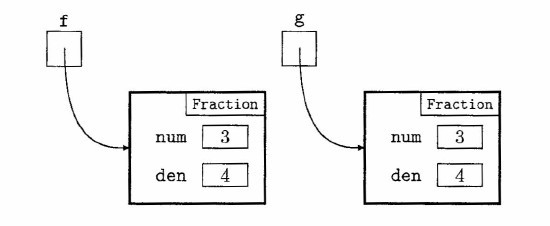
Example 3 If f and g are as shown in the diagram, then the expression f == g would have the value false because f and g refer to distinct objects stored in different locations in memory. The fact that each of those objects represent the same fraction is irrelevant.

If we want to perform a comparison of two objects based on the contents of their fields, we usually do what we have been doing with strings - use a boolean-valued instance method called equals. To be consistent with the equals methods in the classes of Processing's API, any equals method that we write should be an instance method with one explicit parameter that returns false if the explicit parameter has the value null.

Example 4 The following method will return true if and only if two Fraction objects have identical fields. The method first checks that the explicit parameter object is not null*. If it is not, the method then checks that each of the fields of the two objects are equal. *There is no need to check that the implicit object is not null as Processing requires that an instance method be given an instance of an object as an implicit parameter and null is not considered to be an instance of an object. Any attempt to use null as the value of an instance variable would produce an error message. boolean equals (Fraction other) { if (other!=null && num==other.num && den==other.den) return true; else return false; } If you look carefully at this method, you will notice that it returns true when the boolean expression that controls the if statement is true and it returns false when that expression is false. We can take advantage of this observation to shorten the method definition by simply returning the value of the expression. boolean equals (Fraction other) { return other!=null && num==other.num && den==other.den; } We could use this method in contexts like the following: if (p.equals (q)) ...

An equals method need not require that all fields be equal. The method can apply whatever criteria we choose to consider for equality. For objects of the Fraction class, for example, we might consider that two objects are equal if the ratios of the num and den fields of the objects are equal.

If we do not write our own equals method, Processing supplies a default version for us, for any type of object that we define. Unfortunately, Processing's default equals method is fairly useless as it only uses == as its criterion for equality. To get something more useful, we must override the default method by writing our own as we have in Example 4.

To display values, we have been using the methods print and println. These methods automatically convert primitive values (like int or double) to String values for printing. If we want to display objects, we can do so in the same way. For any class, Processing automatically calls an instance method toString provided for this purpose.

Example 5 Consider the following method: void setup () { Fraction f = new Fraction(2,3); println(f); } On the computer on which this book was written, on the day on which this section was written, this method produced the output Fraction@1cc7c5

The toString method that Processing provides as a default returns a string that contains the identifier of the class together with a memory reference to the current object. The memory reference may vary from one machine to another and from one day to another on the same machine. As we did with the default for the equals method, we can override the default toString method with our own.

Example 6 Suppose we add the following method to our Fraction class. String toString () { return num + "/" + den; } Now, if we were to run the program in the previous example, Processing would use our toString method rather than the default. The output from the program would be 2/3 the numerator and denominator of the object in a form that looks like a fraction.

For each class that you create, you should write a toString method that overrides the default method. Even if you don't plan to use such methods in your programs, they can be very useful for debugging while you are developing a program involving objects. For each case, choose a form for the string that makes the information clear.

Exercise 6.4 If p and q are both variables of type Fraction, under what circumstances will the expression p == q have the value true? Suppose that p and q are both of type Fraction with p representing 2/3 and q representing 1/6. Draw a diagram like those shown in the text to illustrate this situation. If the statement p = q; is executed, draw a diagram to illustrate the result. The diagram shows a Circle object of the type that we have been using in exercises throughout this chapter. 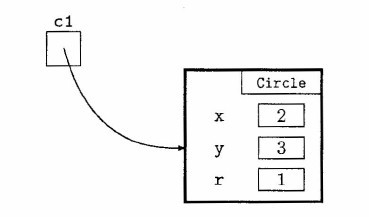Write a fragment to create a new reference, c2, to the same object. Write a fragment to create a new Circle object c3, with the same centre and radius as c1. Draw diagrams to illustrate the results of executing the code in parts (a) and (b). What is the value of the expression cl == c2? What is the value of the expression c1 == c3? Write a boolean instance method called equals that returns true if and only if one Circle object is equal to another one. Write a toString method for the Circle class. For a Circle object with x = 3, Y = -4, and r = 2, the toString method should return a String with the value: "centre: (3,-4) radius: 2". You have been hired by a wicked witch with a strong interest in children. The program that she uses to help her maintain records has a class Child that contains the fields int height; // height in cm double mass; // mass in kg The witch wants you to write an equals method for the class. The witch considers two Child objects to be equal if their heights differ by no more than 2 cm and their masses differ by no more than 0.5 kg. Write a definition of an equals method for the Fraction class. Your method should return true if and only if the Fraction objects being compared represent equivalent fractions.