6.10 Review Exercises 6

Exercise 6.10

What is the difference between a class and an object?

What is the difference between the declaration of a class field and the declaration of an instance field?

What is the difference between a call to a class method and a call to an instance method?

Suppose that a complex number z = a-s-bi is represented by an object of the form shown in the diagram

Write a definition for a class Complex that contains
1. private double fields re and im for the real and imaginary parts of a number,
2. a constructor method that could be called by the statement
```
Complex z = new Complex(2.7,-1.1); 
```
  to create an object that represents the complex number 2.7 - l.li,
3. a constructor method with no parameters that creates a Complex object representing the number 0,
4. an instance method that finds the modulus of a complex number,
5. an accessor method that returns the value of the real part of a complex number.

Suppose that the following fragment is part of a method in the Complex class developed in the previous question. Draw diagrams to illustrate the result of executing the fragment.
```
Complex z1, z2, z3;
z1 = new Complex(2,-2);
z2 = new Complex();
z3 = z1;
z2.re = z3.im + 3;
z2.im = 2*zl.im;
z3.im = z1.re / 2; 
```
Write an instance method harmonicSum for the Fraction class discussed throughout this chapter. The method should have one int parameter, n. It should set its implicit parameter to the value of the fraction found by adding the terms of the harmonic series

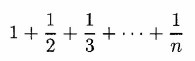
The fraction should be reduced to lowest terms. If n < 1, then the fraction should be set to .

Write a class Lock that could be used to create electronic lock objects. Each lock may be in either an open (unlocked) or a closed (locked) state and each one is protected by its own integer key which must be used to unlock it. The class should contain the following methods.
- ```
public Lock (int key) 
```
  Create a lock that is initially open.
- ```
public void close () 
```
  Close the lock.
- ```
public boolean isOpen () 
```
  Return true if and only if the lock is open.
- ```
public void open (int key) 
```
  Open the lock if and only if the parameter key matches the lock's own key. If the lock is closed and the keys do not match, count the failed attempt. If the same lock receives three or more failed attempts in a row, print the message "ALARM".
The following main method illustrates how the Lock class should work.
```
public static void main (String[] args)
{
   Lock lockl = new Lock(111);
   Lock lock2 = new Lock(222);
   

   lock1.close();
   lock2.close();
   

   System.out.println(lock1.isOpen()); // prints false
   lockl.open(123); // fails to open lockl
   lockl.open(456); // fails to open lockl
   lock2.open(222); // opens lock2
   lockl.open(789); // fails - prints ALARM
   lock1.open(111); // opens lock1
} 
```

Projects

Suppose that rectangles in a Cartesian plane are represented by a class Rectangle that has four private fields as shown:
```
class Rectangle
{
   private int left; // x-coordinate of left edge 
   private int bottom; // y-coordinate of bottom edge
   private int width; // width of rectangle
   private int height // height of rectangle
 
```
1. Write a constructor method that has four parameters representing the four fields of the class. The constructor should replace any negative length parameters with zero.
2. Write a toString method for the Rectangle class. For the rectangle with lower left corner located at (3,2) and having width 4 and height 5, the method should return "base:(3,2) w:4 h:5".
3. Write an instance method, area, that returns the area of a rectangle.
4. Write an instance method, perimeter, that returns the perimeter of a rectangle.
5. Write a class method, intersection, that has two Rectangle parameters. The method should return the rectangle formed by the area common to the two rectangles. If they do not intersect, the method should return the rectangle whose instance fields are all zero. If the rectangles touch, the method should return a "rectangle" of zero width or zero length.
6. Write a class method, totalPerimeter, that has two Rectangle parameters. The method should return the total perimeter of the figure formed by the two rectangles. It should only count as part of the perimeter those portions of the edges of a rectangle that are on the exterior of the resulting figure. If one rectangle is completely contained by the other, then the method should return the perimeter of the outer rectangle. If the rectangles do not intersect, then the method should return the sum of the individual perimeters.
7. Write an instance method, contains, that has one explicit parameter of type Rectangle. The method should return true if every point of the rectangle determined by the explicit parameter is on or within the rectangle determined by the implicit parameter. It should return false otherwise.

Java provides a class BigInteger in the package java.math that allows us to perform arithmetic on integers that are arbitrarily large. The class includes the following features (plus many others):
- Two class fields contain the Biglnteger representations of zeroand one.
```
public static final Biglnteger ZERO
public static final Biglnteger ONE 
```
- There is a constructor that creates a Biglnteger from a given string. It has the header
```
public Biglnteger (String s) 
```
  The string s consists of a sequence of one or more decimal digits that may be preceded by an optional minus sign. No other characters are permitted.
- Instance methods for performing arithmetic include the following:
```
public Biglnteger add (Biglnteger other)
public Biglnteger subtract (Biglnteger other)
public Biglnteger multiply (Biglnteger other)
public Biglnteger divide (Biglnteger other)
public Biglnteger remainder (Biglnteger other)
public Biglnteger gcd (Biglnteger other) 
```
  In each case, the method whose identifier is <op> returns a Biglnteger whose value is this <op> other. The method gcd returns the greatest common divisor of this and other.
- A method compareTo compares two Biglnteger values. The method has header
```
public int compareTo (Biglnteger other) 
```
  The method returns -1, 0, or 1depending on whether the implicit Biglnteger object is less than, equal to, or greater than other. It can be used to implement any of the six relational operators (<, <=, >, >=, ==, or !=) by writing expressions of the form
```
a.compareTo(b) <op> 0 
```
- A toString method returns a string representation of a BigInteger value. The method has the header
```
public String toString () 
```
- An equals method tests two BigInteger objects for equality. The method has the header
```
public boolean equals (Biglnteger other) 
```
Use the BigInteger class to create a BigFraction class. The class should contain features that parallel those in the Fraction class of Section 6.8 (Putting the Pieces Together). Write a main method, in another class, that tests your BigFraction class thoroughly.

In 1843 William Rowan Hamilton extended the notion of a complex number to that of a quaternion. Complex numbers contain the value i with the property that i^2 = -1 while quaternions contain values i, j, and k with the following properties:

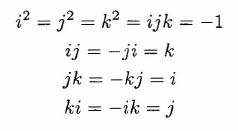
Just as a complex number z can be written in the form z = a + bi where a, b ∈ R, a quaternion q can be written in the form q = w + xi + yj + zk where w, x, y, z ∈ R. We can also represent a quaternion as an ordered quadruple-of real numbers [w,x,y,z]. Sometimes it is useful to represent a quaternion as a combination of a scalar s = w and a vector v = [x, y, z]. Thus, the following are all equivalent:

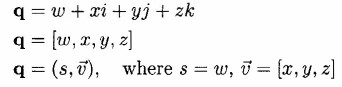
We will be interested in a number of operations involving quaternions.
- Addition
  Given two quaternions
  
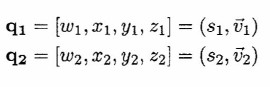
  their sum is:
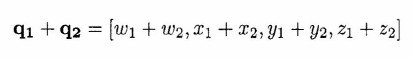
- Multiplication
  The product of quaternions q1 and q2 is:
  
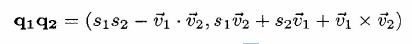
  where V1.V2 (the dot product) and V1xV2 (the vector product) are defined as follows:
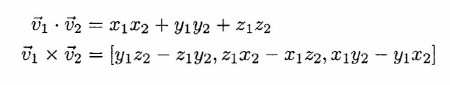
- Scalar Multiplication
  A quaternion q can be multiplied by a real number to give a quaternion result. If c ∈ R and q = w + xi + yj + zk, then
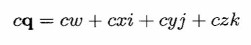
- Conjugation
  If q = w + xi + yj + zk, then the conjugate of q is
- Finding Magnitude
  The size or magnitude of a quaternion q is
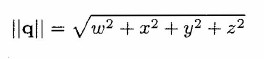
- Inversion
  The inverse of a quaternion q is
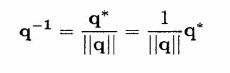
Quaternions are useful in computer graphics for the representation and calculation of rotations of graphical objects. Suppose that we are given a point P = (x, y, z) and we want to determine its image P' after a rotation through an angle Θ about a direction defined by a unit vector u. We first obtain a quaternion representation of the point P by letting

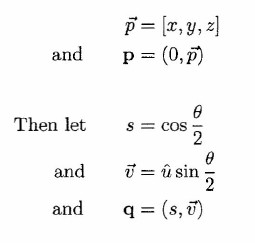
If we now find the product

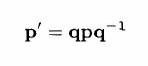
this product will have the form

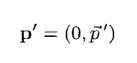
where the components of p' are the coordinates of the image P' of the original point P.

You are to create two classes in two different files. In a file called Vector3.java, you should create fields and methods to implement three-dimensional vectors. This class should begin with the following field definitions:
```
class Vector3
{
   private double x;
   private double y;
   private double z;
   ..
} 
```
You must also write a number of methods for the class. These should include (but are not limited to) the following:
- A constructor with three double parameters representing the fields x, y, and z.
- A toString method that, for a vector with components x, y, and z, returns a string of the form:
  "[x,y,z]"
- Accessor methods getX, getY, and getZ that return the values of x, y, and z respectively.
- An instance method dotTimes with one explicit parameter of type Vector3. The method should return the value of the dot product of its implicit and explicit parameters.
- An instance method vecTimes with one explicit parameter of type Vector3. The method should return the value of the vector product of its implicit and explicit parameters (in that order).
- An instance method scaleTimes that has one double parameter. The method should return a vector that is the result of multiplying the double parameter by the implicit vector object.
- An instance method unit with no explicit parameters. The method should return a normalized (unit) vector that has the same direction as the implicit parameter. If the parameter represents the zero vector, the method should return the zero vector.
In a separate file, called Quaternion.java, you are to create a class to implement quaternions. This class should begin with the following field definitions:
```
class Quaternion
{
   private double y;
   private double x;
   private double y;
   private double z;
   ..
} 
```
You are to write the following constructors and methods to be added to the class:
- A constructor method that has four parameters representing the fields w, x, y, and z.
- A constructor that has two parameters: a double value representing the scalar part of a quaternion and a Vector3 object representing the vector part.
- A constructor with no parameters that creates an instance of a unit quaternion, with a scalar of one and vector components all set to zero.
- A toString method that returns a string containing the object's components as a scalar, s, and a vector, v. For the quaternion q = [3.23,2,-0.625,3.56], the method would return the string
  "s: 3.23 v: [2.0,-0.625,3.56]"
- An instance method conjugate that returns the conjugate of its implicit parameter.
- An instance method magnitude that returns the magnitude of a quaternion.
- An instance method times that returns a Quaternion object which is the product of the implicit object times the explicit object (in that order).
- An instance method inverse that returns the inverse of its implicit parameter.
- An instance method getVector that returns, as a Vector3 object, the vector portion of its implicit quaternion object.
- A class method image that finds the image P' of a point P under a rotation. The header of the method is
```
public static Vector3 image (Vector3 p, Vector3 u, double theta) 
```
  Here p is a vector whose components are the coordinates of the point P, u is a vector giving the direction of the axis of the rotation, and theta is the angle, in radians, through which the rotation is to take place. The vector returned by the method has components that are the coordinates of the image point P'.
You should create your own main method to test your classes thoroughly.