Exercise 4.8

1. What will be printed by each fragment?

   1. for (i = 0; i <= 5; i++)
         System.out.println(i*i); 

   2. n = 3;
      do
         System.out,println(++n);
      while (n < 8); 

   3.  for (i = 25; i > 0; i -= 4)
         System.out.println(i); 

   4. for (i, = j = 1; i < 5; i++)
      {
         j *= i;
         System.out.println(j);
      } 

   5. n=26;
      while (n != 1)
      {
         if (n % 2 0)
            n /= 2;
         else
            n = 3 * n + 1;
         System.out.println(n);
      } 

2. Describe in a few words what would be stored in the variablevalue afterexecution of each fragment.

   1. for (i = value = 0; i <= 10; i++)
         value += i; 

   2. n = In.getlnt();
      value = 0;
      while (n % 2 == 0)
      { 

      value++;
         n /= 2; 

      }

   3. n = In.getInt 0;
      value = 0;
      do
      {
         value += n % 10;
         n /= 10;
      }
      while (n > 0);

3. A prime number is a positive integer that has exactly two distinct divisors - one and the number itself. For example, 17 is a prime number because it is divisible only by 1 and 17. Write a program that reads an integer and then prints a message stating whether or not it is a prime number.
4. The number 153 has the property that it is equal to the sum of the cubes of its digits: 1³+5³ +3³ = 15³. Write a program that will find all the three-digit natural numbers that have this property.
5. Write a program that prompts the user for a natural number and, once one has been supplied, finds and prints all of its exact divisors.

6. The number 6 is said to be a perfect number because it is equal to the sum of all its exact divisors (other than itself).

   6=1+2+3
   Write a program that finds and prints the three smallest perfect numbers.
7. 1. Write a program that could be used to playa simple game. The program should first ask one user to supply a positive integer less than 1000. Once this user has provided an appropriate value, the program should than ask a second user to guess the number that was given by the first user. After each incorrect guess, the program should tell this user whether the guess was too low or too high and ask for another guess. This should continue until the second user has found the correct number. The program should then print the number of guesses that the second user needed to determine the number.
   2. What guessing strategy will minimize the expected number of incorrect guesses?

8. Let n be a positive integer consisting of the digits d_k ... d_Id_o. Write a program that reads a value of n and then prints its digits in a column, starting with do. For example, if n = 3467, then the program should print

   
9. Rewrite the program in the previous question so that it prints the digits of n in the opposite order, starting with d_k and working down to d_o.

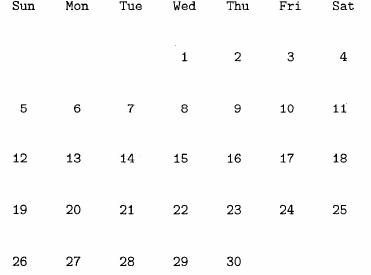
10. Write a program that takes as input the number of days in a month and the day of the week on which the first of the month occurs. The program should produce a display of the calendar for that month in standard form. For example, if there are 30 days in the month and the first day of the month is Wednesday, the input would be 30 and Wednesday, while the output should be similar to the following.

    
11. Write a program that computes the amount to which periodic deposits of $1 will grow at a given rate of interest and for a given length of time. The program should prompt the user to provide an interest rate as a percent (from 0 to 20) and a number of compounding periods (from 0 to 50). The program should then produce a table with appropriate headings showing the amount to which $1 per period (paid at the start of each period) has grown for 1,2,3, ... ,n periods where n is the value provided by the user. The program should reject invalid input, continuing to prompt the user until valid data have been provided. (Do not attempt to screen for non-numerical input.) Amounts in the table should be rounded to the nearest cent.

12. Write a program that first prompts the user for a value of x, reads x (as a double) and then computes and prints the value of eX without using either of the methods exp or pow from the Math class. The value of e^x is given by the following power series

    .

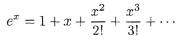13. In computing the value of e^x, your program should continue to add terms of the power series until it reaches a term whose absolute value is less than 10^-15 times the absolute value of the sum of the previous terms.

    

    The symbol n! is read as n factorial. If n is a positive integer, then

14. Write a program that reads a positive integer and then checks to see whether or not the integer is divisible by 11. For the divisibility test, use the following algorithm, based on one given by the mathematician Charles S. Dodgson (also known as Lewis Carroll).

    • As long as the number has more than one digit, shorten it by deleting the units digit and subtracting this digit from the resulting number.
    • The original number is divisible by 11 if and only if the final number is equal to zero.
    You may assume that the input is valid and that it can be stored as a long value. Output from the program should consist of the original number followed by any shortened numbers obtained by applying the algorithm followed, finally, by a message stating whether or not the original number was divisible by 11.As an example, input of 48070 should produce like the following:
    

15. The diagram shows a unit square in the Cartesian plane and a quarter circle of radius one, centred at the origin.

    
    1. Show that, if a point is chosen at random within the square, the probability that it will also be inside the quarter circle is π / 4.
    2. Write a program that repeatedly generates the coordinates of a random point within the square and determines whether or not the point also lies inside the quarter circle. The program should repeat the process 10 000 times. After every 1 000 repetitions, it should use the results to determine and print an estimate of the value of π (based on all repetitions up to that point).

16. Assuming that there are 365 days in a year and that the probability that a person will be born on a given day is 1/365, we can calculate the probability that, in a group of five people chosen at random, at least two will have the same birthday, as follows:

    We start by calculating the probability that all five have different birthdays. This will be

    

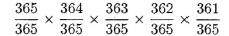
    The reasoning here is that the first person could be born on any of 365 days; the second person, to have a different birthday, could only be born on 364 out of 365 days; the third person, to have a birthday different from either of the first two, could only be born on 363 out of 365 days; and so on to the fifth person. Now, to find the probability that at least two people in a randomly chosen group of five have the same birthday, we simply subtract the above expression from 1 to obtain.

    

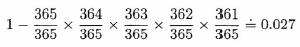
    Write a program that produces a table showing the minimum number of people that would be required so that the probability of at least two people in a randomly chosen group having the same birthday is at least 0.1,0.2, ... ,0.9,1.0

17. Write a program that will determine the roots of equations of the form ax² + bx + c = O. The program should repeatedly prompt the user for values of a, b, and c. For each set of values, the program should solve the corresponding equation, if it has a solution, or print an appropriate message, if it has no solution. The program should be able to cope with coefficients that produce either real or complex roots. It should also be able to give appropriate results if one or more of the coefficients are equal to zero. The program should be interactive. The form of the exchange between a user and a computer is shown in the following example.
    
18. Write a program that will perform the four basic arithmetic operations (addition, subtraction, multiplication, and division) on pairs of fractions, producing answers in standard fractional form. Specifically, your program should repeatedly perform the following actions.
    • Read a character representing an operation. This will be one of the characters +, -, *, i, or $. The $ signals the end of the data; reading it should cause the program to terminate.
    • Read four integers representing the numerator and denominator of a first fraction followed by the numerator and denominator of a second fraction.

    • Perform the indicated operation and print the results in the appropriate form as illustrated in the examples that follow.

      Here is an example, determining the product 57 x 86 = 4902:

      

19. Write a program that prompts the user for a multiplier and a multiplicand and then uses the Russian Peasant Algorithm to determine the product. Your program must also show the intermediate steps the algorithm takes by printing out any row where an addition is required in the first column. Your program should continue prompting the user for input until two zeros are entered. This should terminate the program. If a user provides negative values for either the multiplier or the multiplicand, these should be rejected. If one value is zero and the other is positive, the program should give the correct result without using the algorithm. Using the example above, your program should function as shown in the following sample: