12.6 Binary Search Trees

     A binary search tree is a binary tree in which the nodes are arranged using some key contained in each node. If each key is unique, then we can define the structure of the ADT binary search tree as: a binary tree in which the keys of nodes in the left subtree are all less than that of the root, the keys of nodes in the right subtree are greater than that of the root, and both subtrees of the root are binary search trees. (If keys are not unique, it is easy to make appropriate changes to the definition.)
     As its name suggests, the structure of a binary search tree allows us to search easily an item stored in the tree. We show how to so in the next example.

Example 1

Consider the following binary search tree in which names are used as keys.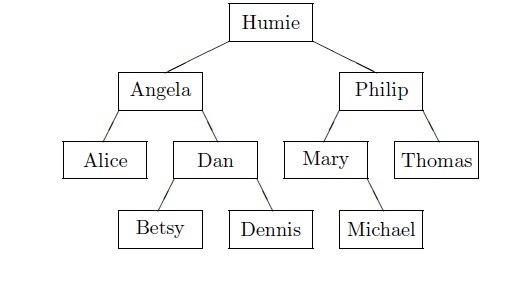

To search for Betsy in this tree, we begin by looking at the root, comparing Betsy to Humie. Since Betsy precedes Humie, and all keys that are less than Humie are in the left subtree, we move to the left subtree. We continue the process by comparing Betsy to Angela and moving to Angela's right subtree, comparing Betsy to Dan and moving to Dan's left subtree, where we finally find Betsy.

If we attempted a search for an item that was not in the tree, then the process outlined here would eventually reach a dead end by following a path to an empty subtree. For example, a search for Tina would lead us to Burnie, Philip, and Thomas. Since the right subtree from Thomas is empty, the search ends in failure.


An algorithm for performing a search in a non-empty binary search tree can take the following form. 
To SEARCH A NON-EMPTY TREE
   if item is at root
      search is successful
   else if item < root
      if left subtree is empty
         search fails
      else
      SEARCH THE NON-EMPTY LEFT SUBTREE
   else
   if right subtree is empty
      search fails
   else
      SEARCH THE NON-EMPTY RIGHT SUBTREE

     As usual, when we implement this algorithm in Java, we use a nonrecursive version (in an outer class) to handle the possibility that the entire tree is empty and a recursive version (in an inner class). The implementation is left as an exercise.
     To insert a new node in the tree, we follow an algorithm similar to that used in our search. The recursive part of the algorithm is shown here. 
To INSERT IN A NON-EMPTY TREE
   if item precedes root
      if left subtree is empty
         insert as left child of this node
      else
         INSERT IN NON-EMPTY LEFT SUBTREE
   else
   if right subtree is empty
      insert as right child of this node
   else
      INSERT IN NON-EMPTY RIGHT SUBTREE

Example 2

This non-recursive method, for the Tree class, starts insertion by creating a new node containing the item to be inserted and either inserting it into an empty tree or calling a recursive method to insert it into the non-empty tree. The method uses a constructor from the Node class, not shown here. 
public void insert (int item)
{
   Node newNode = new Node(item,null,null);
   if (root == null)
      root = newNode;
   else
      root.insert(newNode);
}
This recursive method inserts a new node into a non-empty binary search tree. 
void insert (Node newNode)
{
   if (newNode.info < info)
      if (lChild == null)
         lChild = newNode;
      else
         lChild.insert(newNode) ;
  else
  if (rChild == null)
      rChild = newNode;
   else
      rChild.insert(newNode);

     Once we have created a binary search tree, it is very simple to print the values of the nodes in order by the keys. Since the values in the left/right subtree of any node precede/follow that root's values, they should be printed before/after the value of the root. This is exactly what we get when we print a binary tree using an inorder traversal.

Exercise 12.6

  1. In our definition of a binary search tree, we required that each node have a unique key. Suggest a modification of the definition that could be used if keys in nodes are not necessarily unique.


  2. Referring to the binary search tree shown in Example 1, which nodes would be examined if we were to search for the following names in the tree?

    (a) Michael           (b) Barry

    (c) Nemanja         (d) Dennis


  3. Referring again to the tree of Example 1, if we were to insert Tina in the tree, she would go in as the right child of Thomas. Determine where the following names would be inserted.

     (a) Jane      (b) Polly


  4. A binary search tree is to be created using the names of the planets. Draw a diagram showing the resulting binary search tree if the items are inserted in the following order into an initially empty tree.

    Mercury  Venus  Earth  Mars  Jupiter  Saturn  Uranus  Neptune  Pluto


  5. (a) What would happen if the insertion methods of Example 2 were used to attempt to insert an item that was already in the binary search tree?

    (b) How would the insert method of the Node class have to be modified so that an attempt to insert an item that is already in the tree would be denied and a warning message would be produced?


  6. Write a pair of instance methods, both called contains and both having a single int parameter called item, that search for item in a binary search tree. The methods should return true if and only if item is found in the tree.