12.2 More Operations on Linked Lists

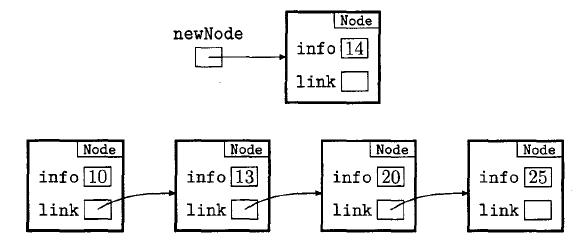
As a first example, let us consider the problem of inserting a new node into a list where the nodes of the list are to be ordered. For the simple list structure that we are using, let us suppose that we want to maintain our lists in ascending order by the info fields of the nodes. To illustrate the problem, consider the portion of the list shown in the next diagram and suppose that we want to insert a node containing the value 14 into its correct position.

The insertion process consists, essentially, of simply changing the appropriate link fields to achieve the structure shown in the next diagram.

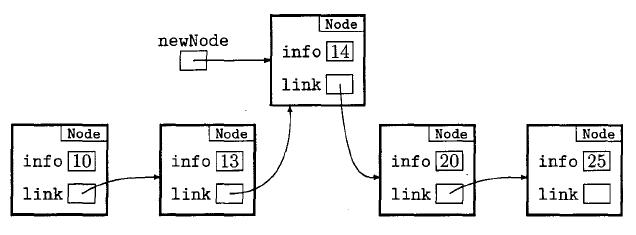
The insertion is carried out in two phases: first the correct location for the new node is found and then links are adjusted so that the node is inserted in the list at this point. To find the correct location for the value 14, we traverse the list using an auxiliary reference variable until we reach the node containing the next largest value, 20. The new node should be inserted just before this one. At this point, it is easy to link the new node to the node containing 20 but we cannot go back along the list to link the previous node, containing 13, to the new node because the links only point forward, not backward. One solution to this problem is to use two auxiliary reference variables in our traversal: one to the current node being examined and the other to the previous node. With these variables we can, if necessary, link the previous node to the new one. This process is implemented in the next example.

Example 1 The method insert will insert a node containing the value item in its info field in a linked list in which the info fields of the nodes are in ascending order. public void insert (int item) { // Find correct location in list for new item Node current = head; Node previous = null; boolean located = false; while (!located && current != null) if (item < current.info) located = true; else { previous = current; current = current.link; } // Create a new node containing item and // referring to correct location in list Node newNode = new Node(item,current); // set link to refer to new node if (current == head) head = newNode; else previous.link = newNode; }

To delete a node containing a particular value in its info field, we must first search the list to find the node that is to be deleted and then adjust links so that this node is snipped out and the reference to the deleted node is redirected to the following node (if there is one). Here again, we must be careful to keep track of the node preceding the one currently being examined so that we can adjust its link, if necessary.

Example 2 This method searches an unordered linked list for a node containing the value item in its info field. If it finds such a node, it deletes it from the list. If there is no such node, the method does nothing; if there is more than one node containing item, only the first is deleted. public void delete (int item) { // Search for node to be deleted Node current = head; Node previous = null; boolean found = false; while (!found && current != null) if (current.info == item) found = true; else { previous = current; current = current.link; } // Perform deletion, if item found if (found) if (current == head) head = head.link; else previous.link = current.link; }

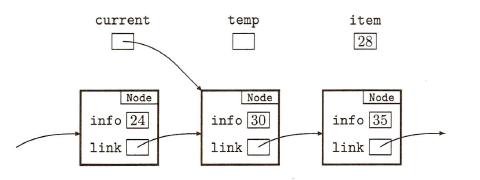
Exercise 12.2 The diagram shows a portion of a linked list. In the diagram, both current and temp are references to objects of the type Node that we have been studying while item is of type int. Draw a diagram, similar to the one given here, illustrating the result of executing the following fragment. temp = new Node(current.info,current.link); current.info = item; current.link = temp; Write an instance method called contains for the List class. The method should have header public boolean contains (int item) The method should return true if and only if its implicit List object contains item. In Chapter 10, we developed a fast searching method (binary search) that took advantage of the fact that a sorted array can be searched much more efficiently than an unsorted one. If the nodes of a linked list are ordered, can we write a form of binary search for a linked list? Justify your answer. Write an instance method deleteAll for the List class. The method should have one int parameter, item. It should delete all nodes in the list that contain item in their info fields. Complete the definition of the method whose header is public boolean isOrderedIncreasing() The method should return true if and only if the info fields of the implicit List object are in strictly increasing order. Assume that the info fields are references to objects for which a compareTo method exists. The technique shown in Question 1 can be used to insert a value into an ordered list without using two auxiliary references. Write an instance method that uses this technique to achieve the same effect as the method shown in Example 1. (Be sure that your method works at both ends of the list.) Write an instance method isldentical for the List class. The method should have the header boolean isldentical (List other) The method should return true if and only if its implicit List object is identical to other.